09 Responses of Digital Filters (22.11.14)

LTI System Characterization

Processing of analog signal with LTI filter

 

● 임펄스 응답

h[n]을 LTI 필터의 임펄스 응답이라고 하면 컨볼루션을 통해 시스템을 특성화 할 수 있다.

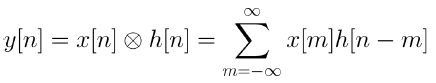
h[n]은 LTI 필터의 시간 영역 응답이다.

 

● 주파수 응답

H(e^jw)는 LTI 필터의 주파수 영역 응답이다.

 

● Difference Equation

LTI 시스템은 아래의 차분 방정식을 충족한다.

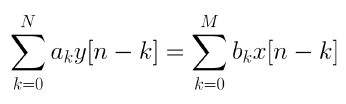
● Transfer Function

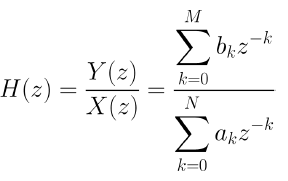
Impulse Response of Digital Filters

H(z)가 1차 극점만 있는 z^(-1)의 유리 함수일 때 아래와 같다.

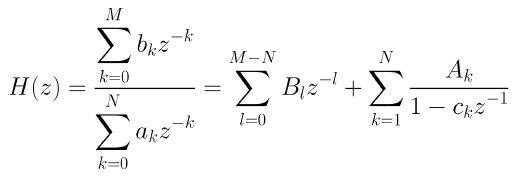
여기서 첫 번째 성분은 M ≥ N인 경우에만 존재한다.

 

시스템이 causal이면 ROC는 |z| > |max| 이어야 한다. 여기서 pmax는 가장 큰 크기의 극점이다.

 

이 ROC에 따르면 임펄스 응답 h[n]은 아래와 같다.

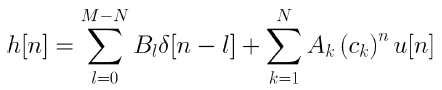
IIR 및 FIR 필터에 해당하는 위의 식의 두 가지 가능한 경우가 있다.

 

● IIR Filter

N ≥ 1이거나 최소 하나의 극점이 있는 경우, h[n]이 무한 기간이기 때문에 시스템을 IIR 필터라고 한다.

 

● FIR Filter

N = 0이거나 극점이 없으면 h[n]이 유한 기간이므로 시스템을 FIR 필터라고 한다.

 

IIR 및 FIR 시스템의 정의는 noncausal 시스템에도 적용된다.

 

Frequency Response of Digital Filters

임펄스 응답 h[n]이 h[n]의 DTFT를 취함으로써 얻어지는 LTI 시스템의 주파수 응답은 아래와 같다.

H(e^jw)는 H(z)를 사용할 수 있는 경우에도 얻는다.

H(z)의 ROC가 단위원을 포함한다고 가정한다.