Discrete Fourier Transform
DFT는 주파수 영역에서 이산 시간 유한 기간 신호를 분석하는 데 사용된다.
x[n]을 외부 0 ≤ n ≤ N-1이 되는 길이 N의 유한 기간 수열이라고 합니다. DFT 쌍은 아래와 같다.
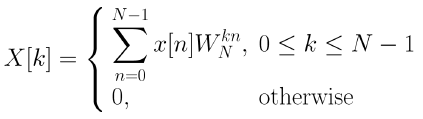
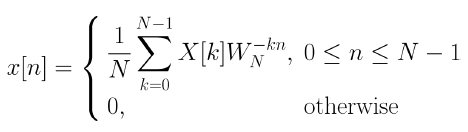
x[n]을 주기 시퀀스 x̄[n]으로 확장하면, X[k] = x̄[k] (0 ≤ k ≤ N-1)이다. 결과적으로 DFT와 DFS는 [0, N-1] 구간 내에서 같다.
Properties of DFT
DFT 쌍은 [0, N - 1] 내에서 DFS 쌍과 동일하므로 인덱스가 간격 밖에 있을 때, x[n] 및 X[k]의 값을 관리하면 속성이 같다.
1. Linearity
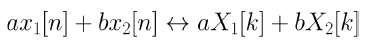
2. Circular Shift of Sequence
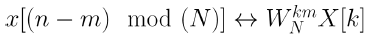
3. Duality

4. Symmetry
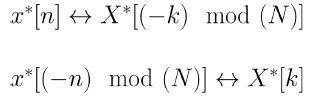
5. Circular Convolution

Fast Fourier Transform
FFT는 DFT 및 역 DFT 계산을 위한 빠른 알고리즘이다.

위의 식에서 각 X[k]는 각각 N 및 (N - 1) 복소수 곱셈 및 덧셈을 포함한다.
모든 DFT 계수를 계산하려면 N^2 복소 곱셈과 N(N - 1) 복소 덧셈이 필요하다.
N = 2^v라고 가정하면 FFT에 해당하는 계산 요구 사항은 0.5Nlog2(N) 복소 곱셈과 Nlog2(N) 복소 덧셈이다.

'Theory > DSP' 카테고리의 다른 글
| 09 Responses of Digital Filters (22.11.14) (0) | 2023.06.14 |
|---|---|
| [MATLAB 실습 07] DFT / FFT (22.11.09) (0) | 2023.06.14 |
| 07 Discrete Fourier Series (22.11.07) (0) | 2023.06.14 |
| [MATLAB 실습 06] z Transform (22.11.02) (0) | 2023.05.02 |
| 06 z Transform - 2 (22.10.31) (0) | 2023.05.02 |




댓글