Inverse z Transform
역 z 변환은 주어진 X(z)와 그 ROC에서 x[n]을 찾는 것이다.
z 변환과 역 z 변환은 ROC가 주어진 경우 일대일 대응이다.

일반적으로 역 z 변환을 평가할 때 사용되는 4가지 기술이 있다.
- Inspection
- Partial Fraction Expansion
- Power Series Expansion
- Cauchy Integral Theorem
Partial Fraction Expansion
X(z)가 z^(-1)에서 유리 함수일 때 유용하다.
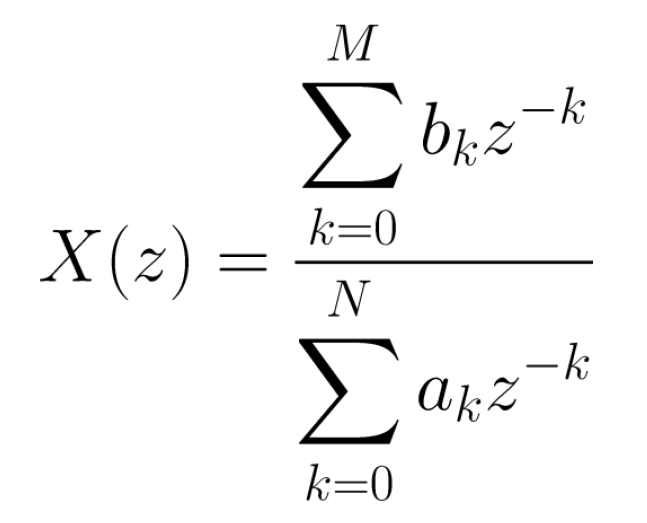
극점 및 영점 결정의 경우 z^(M+N)을 분자와 분모 모두에 곱하는 것이 좋다.
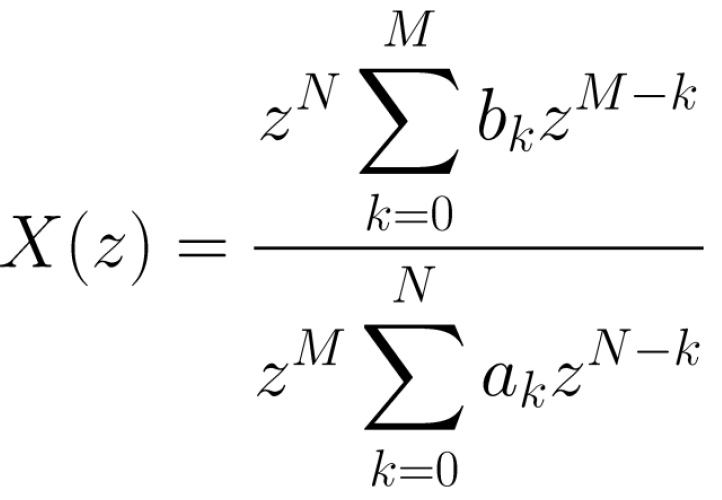
M > N인 경우 z = 0에서 (M - N)개의 pole이 있다.
M < N인 경우 z = 0에서 (N - M)개의 zero가 있다.
Partial Fraction Expension을 얻으려면 첫 번째 단계는 0이 아닌 N개의 극점 c1, c2, ... cN을 결정하는 것이다.
여기서 4가지 경우를 고려해야 한다.
1. M > N이고 모든 pole은 1차인 경우
1차 극점의 경우 모든 {ck}는 별개이다. X(z)는 아래와 같다.
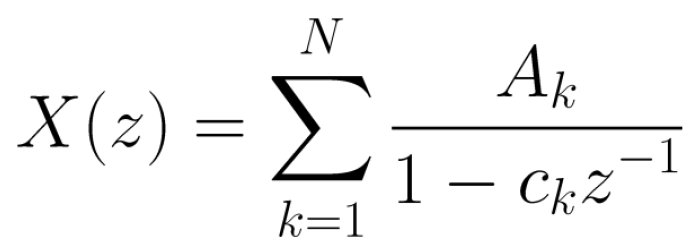
Ak/(1-ck*z^-1)의 각 1차 항에 대해 검사를 통해 역변환을 쉽게 얻을 수 있다.
양변에 (1-ck*z^-1)을 곱하고 z = ck에 대해 평가한다.
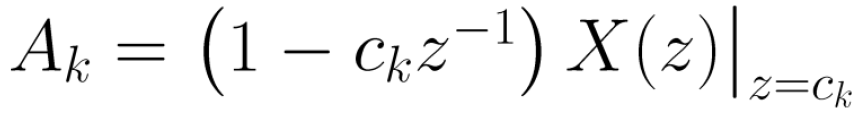
N = 2 > M인 A1을 계산하는 식은 아래와 같다.

z = c1을 대입하면 A1을 얻는다.
요약하면 3단계는
- pole들을 찾는다.
- {Ak}를 찾는다.
- 검사를 통해 분수에 대한 역 z 변환을 한다.
2. M ≥ N이고 모든 극점은 1차인 경우
이 경우에는 X(z)가 아래와 같이 표현될 수 있다.

Bl은 분자를 분모로 길게 나누어서 구하고, 나머지가 분모보다 낮은 차수일 때 나눗셈을 종료한다.
3. M < N이고 다중 차수 극점이 있는 경우
X(z)가 s ≥ 2인 z = ci에서 s차수 극점을 갖는 경우는 동일한 값의 ci를 갖는 s 반복 극점이 있음을 의미한다.
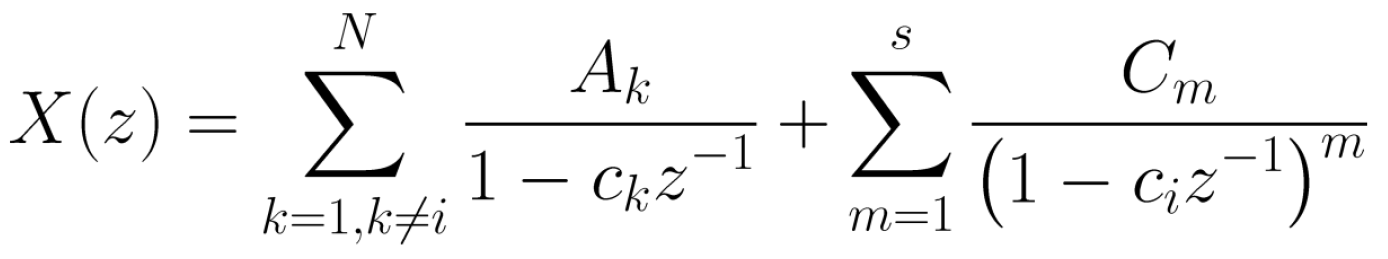
Cm은 아래의 식으로 계산한다.
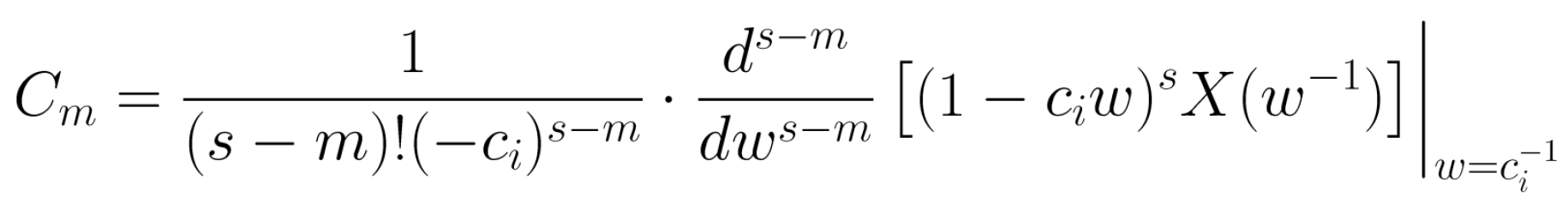
4. M ≥ N이고 다충 차수 극점이 있는 경우
이것은 가장 일반적인 경우이며 X(z)의 Partial Fraction Expansion은 아래와 같다.
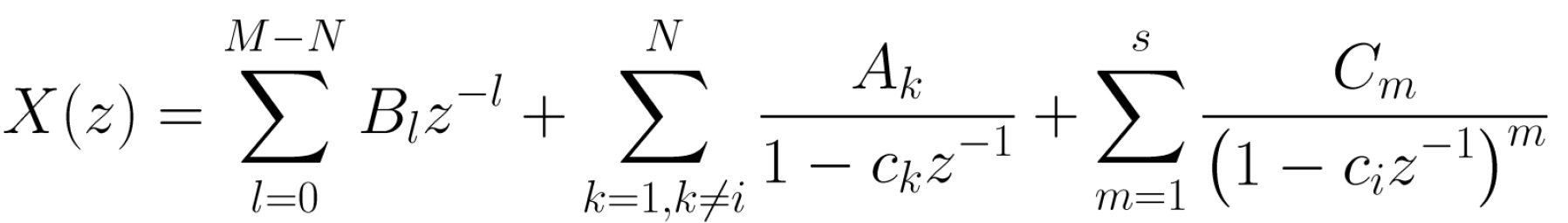
z = ci에서 차수가 s ≥ 2인 다중 차수 극이 하나만 있다고 가정해보자. Case 3과 같이 2개 이상의 다차 극점이 있는 시나리오로 쉽게 확장되고 Ak, Bl, Cm은 Cases 1, 2, 3과 같이 계산할 수 있다.
Power Series Expansion
X(z)를 확장하면 아래와 같다.
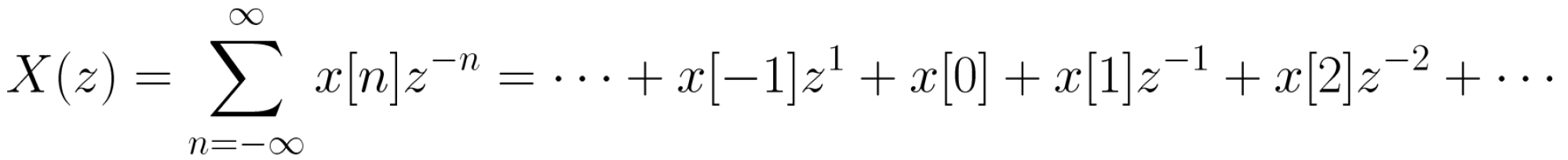
x[n]의 특정 값은 z^(-1)의 적절한 거듭제곱 계수를 찾아 결정될 수 있다.
Properties of z Transform
1. Linearity
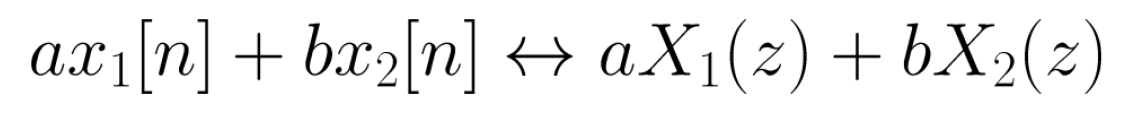
2. Time Shifting

3. Multiplication by an Exponential Sequence (Modulation)
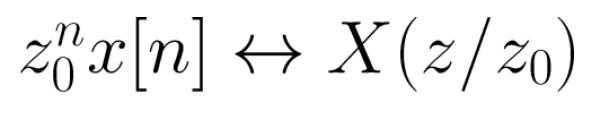
4. Differentiation

5. Conjugation

6. Time Reversal

7. Convolution

Transfer Function of Linear Time-Invariant System
LTI 시스템은 z 변환 표현인 전달 함수로 특징지을 수 있다.
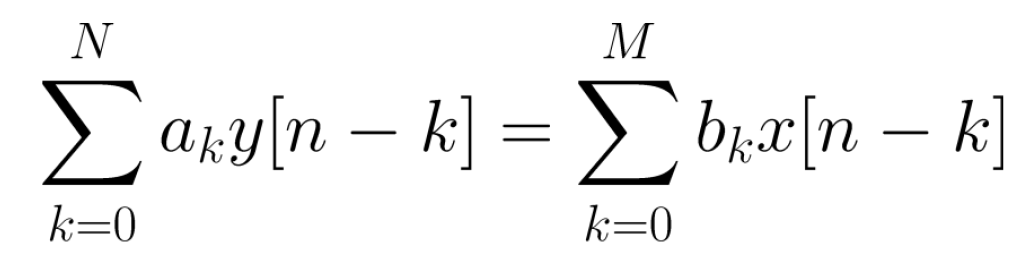
linearity와 shifting properties를 사용하여 위의 식에 z 변환을 적용하면 아래와 같다.

H(z)로 표시되는 전달 함수는 아래와 같이 정의된다.

'Theory > DSP' 카테고리의 다른 글
| 07 Discrete Fourier Series (22.11.07) (0) | 2023.06.14 |
|---|---|
| [MATLAB 실습 06] z Transform (22.11.02) (0) | 2023.05.02 |
| 05 z Transform - 1 (22.10.31) (0) | 2023.05.02 |
| [MATLAB 실습 05] DTFT (22.10.26) (0) | 2023.05.02 |
| 04 Discrete-Time Fourier Transform (DTFT) (22.10.24) (0) | 2023.05.02 |




댓글