DTFT
비주기적 이산 시간 신호를 위한 주파수 분석 도구
x[n]과 X(e^jw)의 DTFT는 아래의 식에서 도출된다.

푸리에 변환에서와 같이 X(e^jw)는 스펙트럼이라고도 하며 주파수 매개변수 w의 연속 함수이다.
X(e^jw)를 x[n]으로 변환하기 위해서는 아래의 역DTFT를 사용한다.


X(e^jw)는 주기가 2π이고 연속적이고 주기적인 성질을 가진다.
X(e^jw)는 일반적으로 복소수이고, 크기와 위상 스펙트럼으로 표현할 수 있다.

두 식 모두 주파수가 연속적이고 주기적인 성질을 가진다.
Convergence of DTFT
x[n]의 DTFT는 아래의 경우에 수렴한다.

x[n]의 z-변환이 R+ < |z| < R- 의 수렴영역(ROC)에 대해 수렴한다고 가정해보자.
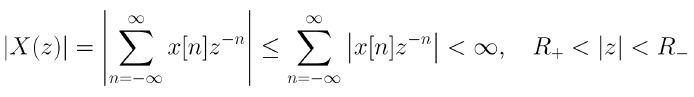
ROC에 단위원이 포함된 경우는 아래와 같다.

이것은 X(e^jw)에 대한 수렴 조건으로 이어지고 z-변환의 P2 속성을 증명한다.
h[n]을 LTI 시스템의 임펄스 응답이라고 하면 아래의 세 문장이 성립한다.
1. h[n]의 z-변환에 대한 ROC는 단위원을 포함한다.
2. 시스템은 stable하고, 아래의 식이 성립한다.
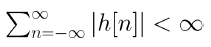
3. h[n]의 DTFT인 H(e^jw)는 수렴한다.
H(e^jw)는 시스템의 주파수 응답이라고도 한다.
Properties of DTFT
DTFT는 변환과 밀접한 관련이 있으므로 해당 속성은 변환의 속성을 따른다. ROC는 DTFT가 존재하기 위해 단위원을 포함해야 하기 때문에 관련이 없다.
1. Linearity
(x1[n], X1(e^jw))과 (x2[n], X2(e^jw))가 DTFT 쌍이면 아래 식이 성립한다.
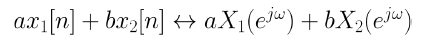
2. Time Shifting
x[n]에서 n0을 이동하면 X(e^jw)에서 e^-jwn0이 곱해진다.
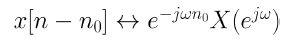
3. Multiplication by an Exponential Sequence
시간 영역에서 x[n]에 X(e^jw)를 곱하는 것은 주파수 영역에서 w0의 이동하는 것과 동일하다.


4. Differentiation
X(e^jw)를 w에 대해 미분하는 것은 x[n]에 n을 곱하는 것과 동일하다.

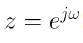
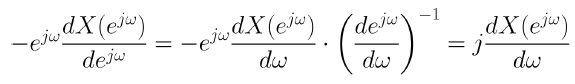
5. Conjugation
x*[n]에 대한 DTFT 쌍은 아래와 같다.

6. Time Reversal
x[-n]에 대한 DTFT 쌍은 아래와 같다.

7. Convolution
(x1[n], X1(e^jw))과 (x2[n], X2(e^jw))가 DTFT 쌍이면 아래 식이 성립한다.
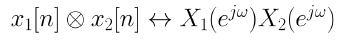
입력 x[n], 출력 y[n] 및 임펄스 응답 h[n]이 있는 LTI 시스템의 경우는 아래의 식이 성립한다.

8. Multiplication
시간 영역의 곱셈은 주파수 영역의 컨벌루션에 해당한다.
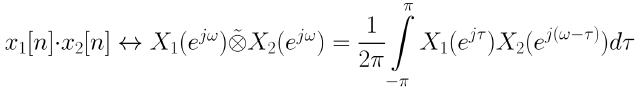
9. Parseval’s Relation
Parseval의 관계는 시퀀스의 에너지를 다룬다.

'Theory > DSP' 카테고리의 다른 글
| 05 z Transform - 1 (22.10.31) (0) | 2023.05.02 |
|---|---|
| [MATLAB 실습 05] DTFT (22.10.26) (0) | 2023.05.02 |
| [MATLAB 실습 04] 이산 시간 푸리에 해석 (22.10.19) (0) | 2023.04.30 |
| 03 Sampling and Reconstruction of Analog Signals (22.10.17) (0) | 2023.04.30 |
| [MATLAB 실습 03] 이산 시간 신호 및 시스템 (22.10.12) (0) | 2023.04.30 |




댓글