푸리에 급수와 푸리에 변환은 아날로그 신호 분석을 위한 도구이다.
기본적으로 시간 영역과 주파수 영역 간의 신호 변환에 사용된다.
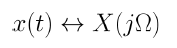
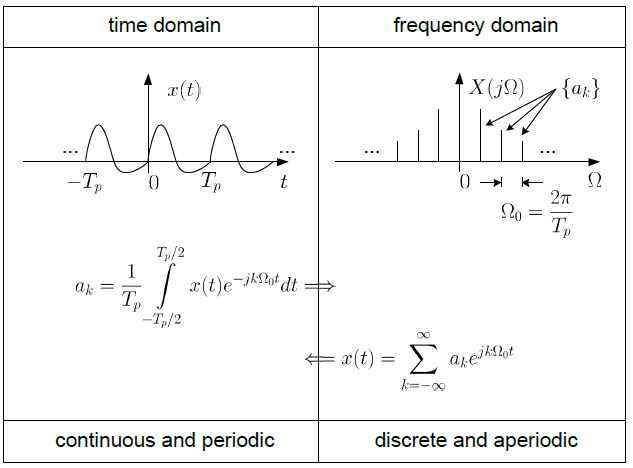
푸리에 급수
- 연속 시간 주기 신호 분석용
- 기본 주파수를 갖는 고조파 관련 정현파를 사용하여 주기적 신호 표현
- 주파수 영역에서 이산 값만을 취함.
연속 시간 함수인 x(t)는 아래와 같이 Tp>0 에서 존재할 때 경우 주기적 함수라고 한다.
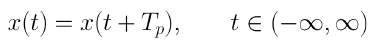
가장 작은 Tp를 기본 주파수라고 한다. 기본 주파수는 아래와 같은 관계를 가진다.
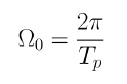
모든 주기 함수는 아래와 같이 푸리에 급수로 확장할 수 있다.
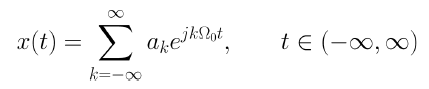
그리고 푸리에 급수의 계수는 아래와 같이 표현할 수 있다.
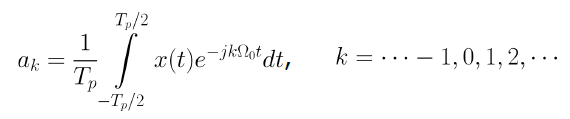
푸리에 급수의 계수는 x(t)의 주파수 표현에 해당하는데, 일반적으로 우리는 크기와 위상을 사용하여 표현한다.
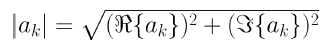
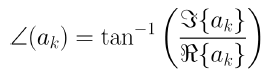
푸리에 변환
- 연속 시간 비주기 신호 분석용
- Ω의 연속적인 범위에서 정의됨.
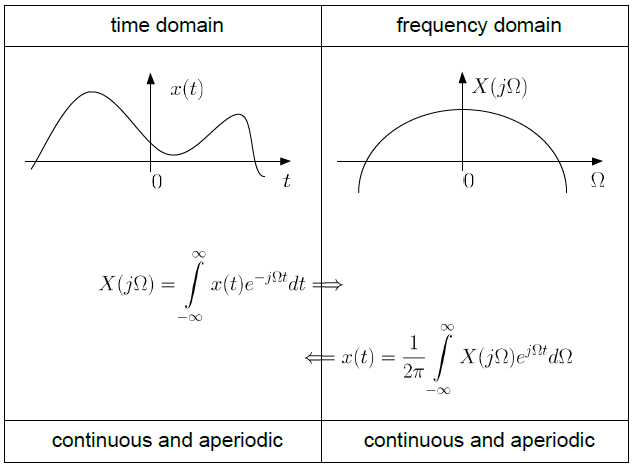
비주기 및 연속 시간 신호 x(t)의 푸리에 변환은 아래와 같으며 스펙트럼이라고도 한다.
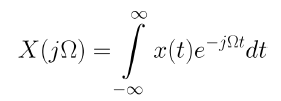
푸리에 역변환은 아래와 같다.
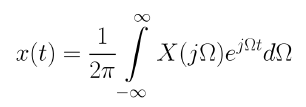
델타 함수는 아래와 같은 특성을 가진다. f(t)는 연속 시간 신호이다.
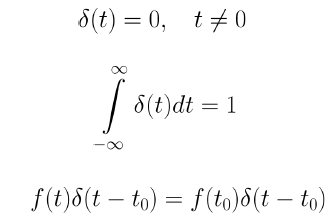
위의 첫번째, 두번째 식들은 델타 함수가 t = 0에서 가장 큰 값 또는 임펄스를 가진다는 것을 나타낸다.
위의 마지막 식은 Shifting Property이다.
델타 함수는 아래와 같이 표현한다.
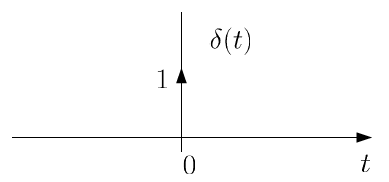
단위 계단 함수 u(t)는 아래와 같이 표현한다.
t = 0에서 값이 0에서 1로 갑자기 변화한다.
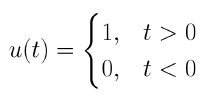
Linear Time-Invariant (LTI) System
Linearity
(x1(t), (y1(t)) 와 (x2(t), (y2(t))의 입력(x)-출력(y)이 있을 때, ax1(t) + bx2(t) → ay1(t) + by2(t) 이다.
Time-Invariance
x1(t) → y1(t) 일 때, x(t - t0) → y(t - t0) 이다.
Convolution
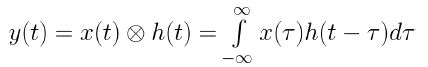
시간 영역의 컨볼루션은 푸리에 변환 영역의 곱셈에 대응된다.
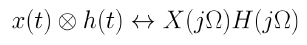
'Theory > DSP' 카테고리의 다른 글
| [MATLAB 실습 03] 이산 시간 신호 및 시스템 (22.10.12) (0) | 2023.04.30 |
|---|---|
| [MATLAB 실습 02] 이산 시간 신호 및 시스템 (22.10.05) (0) | 2023.04.30 |
| [MATLAB 실습 01] 이산 시간 신호 및 시스템 (22.09.28) (0) | 2023.04.30 |
| [MATLAB 연습] 기초 예제 (22.09.28) (0) | 2023.04.30 |
| 02 Discrete-Time Signals and Systems (22.09.26) (0) | 2023.04.30 |




댓글