선형 회귀
독립 변수 x를 사용해 종속 변수 y의 움직임을 예측하고 설명하는 작업
가장 훌륭한 예측선 긋기
정확한 직선을 그려내는 과정
독립 변수 : 독립적으로 변할 수 있는 값 x, 정보 요소
종속 변수 : 독립 변수에 따라 종속적으로 변하는 값 y
단순 선형 회귀 : 하나의 x값만으로도 y값을 설명할 수 있는 경우
다중 선형 회귀 : x값이 여러 개 필요한 경우
최소 제곱법
회귀 분석에서 사용되는 표준 방식
실험이나 관찰을 통해 얻은 데이터를 분석하여 미지의 상수를 구할 때 사용되는 공식
최소 제곱법으로 기울기 a와 y절편 b를 구할 수 있음.
a = [(x - x평균)(y - y평균)의 합] ÷ [(x - x평균)^2의 합]
x의 편차를 제곱해서 합한 값을 분모로,
x와 y의 편차를 곱해서 합한 값을 분자로
놓으면 도출되는 기울기 값
b = y의 평균 - (x의 평균 × 기울기 a)
y의 평균에서 x의 평균과 기울기의 곱을 뺀 값
이 값들을 이용하여 예측 값을 구하기 위한 직선의 방정식 도출 가능
여러 개의 입력을 처리하기에는 무리
평균 제곱근 오차
주어진 선의 오차를 평가하는 오차 평가 알고리즘
여러 개의 입력 값을 계산할 때는 임의의 선을 그리고,
이 선이 얼마나 잘 그려졌는지를 평가하여 조금씩 수정해가는 방법 필요
각 직선의 오차를 계산하고, 오차가 작은 쪽으로 바꾸는 알고리즘 필요
직선의 기울기가 잘못될수록, 직선과 점들의 거리 합은 증가
오차 = 실제 값 - 예측 값
오차의 합 = (실제 값 - 예측 값)^2의 합
마이너스 부호를 없애주기 위함.
평균 제곱 오차(MSE) = 오차의 합 ÷ n
각 오차를 제곱한 값을 사용하면 대용량 데이터를 사용할 경우에 계산 속도 저하
평균 제곱근 오차 = 평균 제곱 오차의 제곱근
평균 제곱 오차와 평균 제곱근 오차는 오차를 계산해서 추론을 평가하는 공식
이 값이 작은 직선을 찾아야 함.
경사 하강법
오차를 줄이기 위해 수정하는 방법
미분 기울기를 이용하여 오차가 가장 작은 방향으로 이동

기울기 a를 x축, 오차를 y축으로 설정하면
기울기 a와 오차 사이에는 이차 함수 형태의 상관 관계를 가짐.
오차가 가장 작은 점은 x가 그래프의 가장 아래쪽의 볼록한 부분에 있는 경우
미분 값이 0인 지점, 기울기가 0인 지점
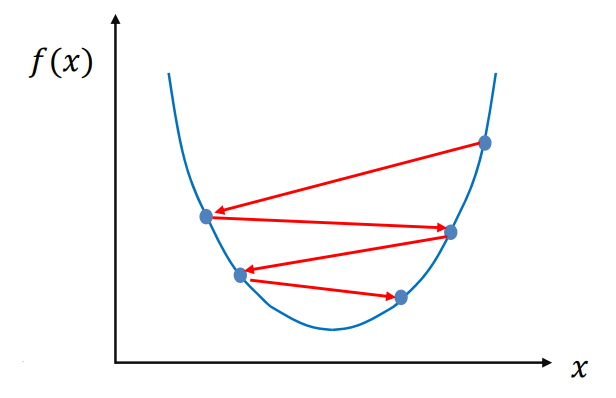
- 한 점에서 미분을 구한다.
- 구한 기울기의 반대방향으로 얼마간 이동시킨 점에서 미분을 구한다.
- 기울기가 +이면 음의 방향
- 기울기가 -이면 양의 방향
- 또 다른 한 점에서 미분을 구한다.
- 3의 값이 0이 아니면 위의 과정을 반복한다.
- 최종적으로 기울기가 0인 한 점으로 수렴한다.
기울기의 부호를 바꾸어 이동시킬 때 적절한 거리를 찾지 못해 너무 멀리 이동시키면
a값이 한 점으로 모이지 않고 위로 치솟는 문제 발생
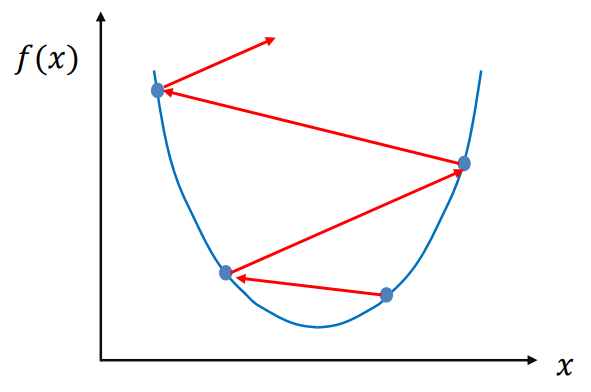
이때 학습률로 이동 거리를 정함.
따라서 경사 하강법은 오차의 변화에 따라 이차 함수 그래프를 만들고
적절할 학습률을 설정하여 미분 값이 0인 지점을 구하는 것
y절편 b의 값도 기울기 a와 같은 성질을 가지고 있기 때문에 최적의 b값을 구할 때 경사 하강법 사용
'Theory > Deep Learning' 카테고리의 다른 글
| 07 모델 성능 검증하기 실습 (0) | 2023.07.11 |
|---|---|
| 05 다중 분류 문제 해결하기 실습 (0) | 2023.07.03 |
| 04 데이터 다루기 실습 (Pandas, Matplotlib, Seaborn) (0) | 2023.07.02 |
| 03 퍼셉트론 / 다층 퍼셉트론 / 오차 역전파 / 활성화 함수 / 고급 경사 하강법 (0) | 2023.07.01 |
| 02 다중 선형 회귀 / 로지스틱 회귀 (0) | 2023.07.01 |




댓글