02 다중 선형 회귀 / 로지스틱 회귀

다중 선형 회귀

더욱 정확한 예측을 위해 정보를 추가해 새로운 예측값을 구할 수 있음.

 

독립 변수 x의 개수만큼 구해야하는 기울기 개수가 증가

 

경사 하강법을 이용하여 기울기들을 구함.

 

 

로지스틱 회귀

참, 거짓을 판단하기 위한 알고리즘

 

참(1)과 거짓(0) 사이를 구분하는 s자 형태의 선을 그려가는 작업

 

로지스틱 회귀를 이용하여 참, 거짓을 판단할 수 있게 하고, 주어진 입력 값들의 특징 추출

이것을 저장하여 모델을 만듬.

 

시그모이드 함수

S자 형태로 그래프가 그려지는 함수

 

y = 1 ÷ [1 + e^(-ax + b)]

시그모이드 방정식에서도 마찬가지로 ax + b를 구해야 함.

a는 그래프의 경사도 결정

a값이 커지면 경사가 커지고, 작아지면 경사가 작아짐.

 

b는 그래프의 좌우 이동 결정

b값이 커지면 좌측, 작아지면 우측으로 이동

 

a값과 b값에 따라 오차 변화

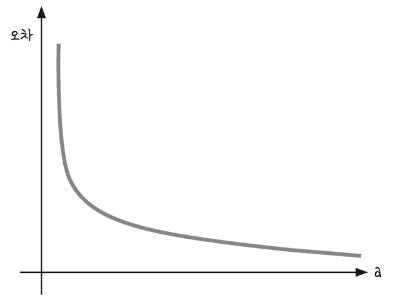
a값이 0에 가까워질수록 오차는 무한대로 커지고, 커질수록 오차는 0에 가까워짐.

b값이 너무 크거나 작으면 오차가 증가

 

시그모이드 함수에서 경사 하강법을 이용하여 a와 b값 구함.

평균 제곱 오차 사용 불가

평균 제곱 오차를 대체할 손실 함수 필요

교차 엔트로피 오차 함수 사용 (로그 함수)

 

실제 값이 1일 때, -logh 함수 사용

예측 값이 1일 때 오차가 0이고, 예측 값이 0에 가까울수록 오차 증가

 

실제 값이 0일 때, -long(1-h) 함수 사용

예측 값이 0일 때 오차가 없고, 1에 가까워질수록 오차 증가

 

두 함수를 한 번에 쓰기 위해서

-{ylogh + (1 - y)log(1 - h)} 함수 사용