03 Sampling and Reconstruction of Analog Signals (22.10.17)

Sampling

연속 시간 신호 x(t)를 이산 시간 신호 x[n]으로 변환하는 과정

x[n]은 샘플링 주기 또는 간격인 T마다 x(t)를 추출하여 얻는다.

x(t)와 x[n]의 관계는 아래와 같다.

개념상으로는 x(t)에서 x[n]으로의 변환은 연속 시간에서 이산 시간으로 변환해주는 변환기로 가능하다.

근본적으로 우리는 x[n]이 x(t)를 고유하게 나타낼 수 있는지 또는 x[n]을 사용하여 x(t)를 재구성할 수 있는지의 여부이다.

아래의 두 가지 조건이 만족하면 재구성할 수 있다.

1. x(t)는 Ω ≥ Ωb에 대해 푸리에 변환 X(jΩ)가 0이 되도록 대역이 제한 (Ωb는 대역폭)
2. 샘플링 주기 T가 충분히 작음.

 

Frequency Domain Representation of Sampled Signal

시간 영역에서, xs(t)는 x(t)에 inpulse train을 곱하여 얻을 수 있다.

impulse train

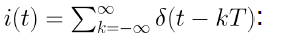
라디안으로 표현하면 Ωs = 2π/T, Fs = 1/T = Ωs/(2π) 이다.

푸리에 변환의 Multiplication Property를 사용하면 아래와 같다.

컨볼루션 연산은 연속 시간 신호와 유사하다.

X(jΩ)/T의 모든 복사본들이 겹치지 않도록 Ωs를 충분히 크게 한 경우에는, Ωs - Ωb > Ωb or Ωs > 2Ωb이고 Xs(jΩ)에서 X(jΩ)를 얻을 수 있다.

하지만 Ωs < 2Ωb와 같이 그렇지 않은 경우 X(jΩ)/T의 복사본들이 겹치게 되고, Aliasing이라는 현상이 발생하여 Xs(jΩ)에서 X(jΩ)를 얻을 수 없다.

 

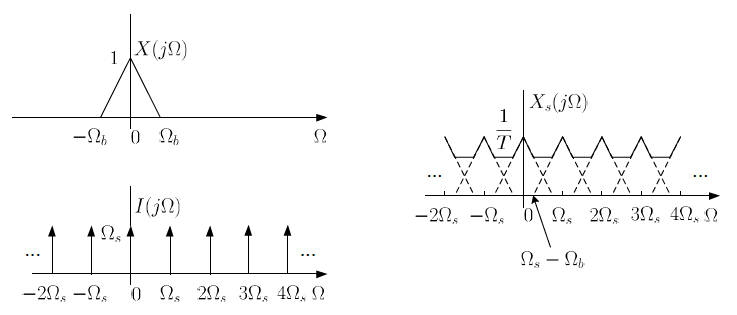
Nyquist Sampling Theorem

x(t)를 아래와 같은 대역 제한이 있는 연속 시간 신호라고 해보자.

그러면 x(t)는 이것의 샘플들인 x[n] = x(nT), n = ... -1, 0, 1, 2, ... 으로 유일하게 결정된다.

대역폭 Ωs는 Nyquist 주파수라고도 하며, 2Ωs는 Nyquist 속도라고 하는데, Ωs는 Aliasing을 피하기 위해 이를 초과해야 한다.

 

Reconstruction

x[n]을 다시 x(t)로 복원하는 과정

H(jΩ)는 Ωb < Ωc < Ωs - Ωb일 때 아래와 같다.

단순하게 만들기 위해 Ωc를 Ωb와 (Ωs - Ωb)의 평균으로 설정하면 아래와 같다.

h(t)를 얻기 위해서 H(jΩ)의 푸리에 역변환을 이용하면 sinc(u) = sin(πu)/(πu)일 때, 아래와 같다.

△ = mT일 때, 시간 이동된 신호는  x[n]을 m 샘플만큼 이동하여 얻는다.

 

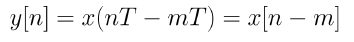
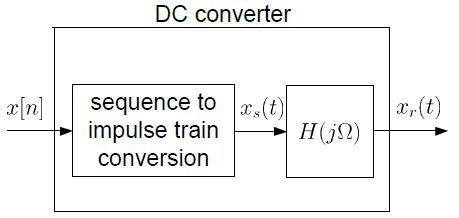
Sampling and Reconstruction in Digital Signal Processing

이상적인 경우

1. CD 컨버터는 x(t)로부터 x[n]을 만들어낸다.
2. x[n]은 이산 시간 영역에서 처리되어 y[n]을 만들어낸다.
3. DC 컨버터는 아래의 식을 이용하여 y[n]으로부터 y(n)을 만들어낸다.

 

현실적인 경우

1. x(t)는 정확하게 대역이 제한되지 않을 수 있다. x(t)를 처리하려면 저역 통과 필터 또는 안티-앨리어싱 필터가 필요하다.
2. 이상적인 CD 변환기는 AD 변환기로 근사치를 만들어낸다.
3. 이상적인 DC 변환기는 이상적인 복원이 불가능하기 때문에 DA 변환기로 근사치를 만들어낸다.
4. x[n]과 y[n]은 양자화된 신호들이다.